Category Archives: Java

neue Features für PVA Carola

Posted on by

Erst war es nur eine Idee, dann wurde es doch Realität: MP3 Metadaten 😉

neue Features für PVA Carola

Als ich in 2021 angefangen habe mit Carola einfachste Anweisungen umzusetzen, kamen schnell möglich Anwendungsfelder ins Spiel z.b. ein naheliegender Gedanke: auf Zuruf Musik abspielen können. Also schaute ich mir meinen Lieblingsplayer QMMP genauer an und der konnte alles per Kommandozeile mitgeteilt bekommen, was für ein Programm, daß eigentlich nur Bashbefehle absetzt naheliegend ist.

Natürlich reicht das nicht, weil man Musik ja auch suchen muß. Wer wie ich jetzt Spotify in Klein zu hause hat, der macht aus der kleinen Aufgabe, mal eben das ~/Musik Verzeichnis zu durchsuchen eine abendfüllende Angelegenheit, weil trotz M2.SSD der Suchvorgang recht lange braucht. Also cacht man trotzdem alles, was man so cachen kann, in diesem Fall alle Pfade und Dateinamen, damit man nur noch eine Datei laden und durchsuchen muß, was nicht mehr Minuten, sondern nur (Bruchteile von) Sekunden dauert.

Jetzt kann man mit einer vernünftigen Benennungsstrategie, recht gute Treffer für Begriffe wie „Queen“, „Elton John“ oder „Alles nur geklaut“ erzielen, aber grundlegende Suchen nach dem Genre fallen weg, weil man das üblicherweise nicht in den Dateinamen schreibt. Da andere Sachen wichtiger waren, blieb es also erst einmal bei dieser simplen Methode.

com.mpatric.mp3agic hat das geändert

Da es noch keine Methode gab, die Musiksammlung durch Metadaten nach Genres abspielen zu lassen, ohne dabei auf andere Audioplayer zu setzen, die nicht das Look&Feel von QMMP hatten, gab es auch keinen Grund die Musiksammlung dahin gehend zu indizieren und die Tags in die MP3-Dateien zu überführen. Wir hatten also ein Henne-Ei-Problem 😉

Github ist ein Hort von Software für fast alles und die JAVA Bibliothek com.mpatric.mp3agic konnte sehr einfach MP3Files auf alles mögliche analysieren. Leider dauerte ein Scan meiner fünfstelligen Sammlung bequeme 10 Minuten. Der Wert ist natürlich für eine Direktsuche viel zu schlecht. Michael, der Autor von mp3agic, konnte die Zeit durch Tipps auf unter 5 Minuten drücken aber auch das war mir noch zu lange.

Java kann eigentlich sehr einfach Subprozesse erzeugen und koordinieren, so daß ein gemeinsamer Datensatz erzeugt werden kann. Hmm.. also was macht man, wenn ein Sequenzielles Verarbeiten von Daten zu langsam ist und genug Prozessoren zur Verfügung stehen? Genau man parallelisiert den Vorgang 😀

Load 12000 – Tendenz steigend!

Ich hatte Carola vor einigen Wochen beigebracht mir den Status des PCs in menschlicher Form mitzuteilen, also nicht einfach stumpf die Load aufsagen, sondern abhängig von der Load entsprechend immer dramatischer klingende Sätze von sich zu geben, bis hin zur Überlastung mit Rotem Alarm und Warnsirenen 🙂 Leider war Carola im ersten, zu erfolgreichem, Versuch selbst die Ursache, so daß es mir leider keinen Kommentar zur Load von 12.000!!! geben konnte 😀

Die CPU brennt? 😀

Eine Load von 12.000 habe ich selbst in 20 Jahren Linux noch nirgendwo gesehen, entsprechend ungläubig habe ich mir die Werte in Top angesehen 😉 Aber wenn man mehr als 10.000 Prozesse gleichzeitig auf 12 unschuldige CPU Kerne loslässt, dann geht die Load relativ schnell nach oben, wenn die IO-Last steigt. Wenn man Anfangs noch 300 Prozesse gleichzeitig von der SSD hat versorgt lassen können, wird das für jeden Prozess der dazu kommt und für den noch kein früherer beendet wurde, immer langsamer, selbst mit „Bis zu 1.000.000 IOPS“ lesend (Samsung Werbung) , weil gar nicht genug Daten am Stück gelesen werden, so ein MP3-File ist ja schliesslich endlich, kann die SSD das nie ausspielen. Dazu kommt noch, daß ein Teil der Daten auf langsameren SATA SSDs oder SATA HDDs gespeichert waren, was die IO-Last deutlich steigert und die Performance drastisch in den Keller zieht.

Anders als bei einem SWAP-of-Death Zustand, ist eine Load von 12.000 kein Problem. Das System läuft bequem weiter, weil die CPU zwar durch IO-Wait gebremst werden, aber alle anderen Prozesse deswegen trotzdem ausgeführt werden können. Das Starten von neuen Anwendungen wird zum Problem, aber z.b. lief die Musik auch störungsfrei durch. Abbrechen kann man die Prozesse so auch leicht.

Wie aus 10+ Minuten 1,5s wurden

Vorteilhaft ist es, die nötigen Blöcke der Dateien bereits im Filecache des OS zu haben, aber um das zu erreichen muß man, welch Wunder, genau diese Blöcke schon einmal gelesen haben. Wenn man das gemacht hat, dann braucht man den zweiten Lauf nicht mehr, weil man das Ergebnis bereits hat. Nur der Statistikfreaks wegen, hier der Benchmark für einen Ryzen 5600X mit DDR4 3200MHz RAM: (bestwert) 1,5s auf 14.000+ Files.

Um den ersten Lauf durchzuführen, braucht man mit der Methode wahnsinnig viel Zeit, fast soviel wie sequenziell, weil durch die vielen Prozesse keiner der Prozesse richtig fertig wird, weil laufend Kontextswitche in der CPU und damit im IO-Controller stattfinden müssen, was höllisch inperformant ist. In der Praxis ist es daher besser ein niedrigeres Limit für die maximale Anzahl an Prozessen zu setzen, so daß die Platten hinterher kommen und die Kerne gut ausgelastet sind. Ich habe da mal 200 als Limit angesetzt.

Ohne Limit dauerte der Vorgang (ungecacht) :

$ time java PVA ‚:“carola erzeuge metadata“‚
erzeuge metadata
found MAKEMETACACHE:

real 15m39,380s
user 0m24,000s
sys 0m9,338s

Mit Limit 200 UND Debugausgabe in Terminal wo er ist…

argument:Das Metacache wurde aktualisiert.

real 0m44,807s
user 0m3,886s
sys 0m2,852s

Mit Limit 200, MIT Filecache UND OHNE Debugausgabe in Terminal wo er ist…

$ time env java PVA ‚:“carola erzeuge metadata“‚
erzeuge metadata
found MAKEMETACACHE:

real 0m3,385s
user 0m3,351s
sys 0m1,800s

Ich denke, das ist ein guter Kompromiss zwischen den Extremen 😉 Ist das Filecache richtig gefüllt, ist es auch egal wieviele Prozesse parallel starten: ob es 200, 2.000 oder 20.000 sind spielt dann keine Rolle mehr. Im ungecachten Zustand ist aber ein wichtiger Faktor, weil die Anzahl der Prozesse die IO-Last reguliert.

Merke: Das Filecache im RAM ist extrem wichtig!

Wie kommt man die Metadaten ran?

Dazu benutzt man am besten PICARD. Ja, ich dachte auch erst an TNG 😉

Mit Picard habt Ihr ein gutes Tool, das schnell, und meisten recht einfach, die Metadaten aus der MusicBrainz Datenbank auslesen kann. Es schreibt dann die Metadaten in die Files.

die Oberfläche von Picard, Links die Dateinamen, oben die Buttonreihe.

MP3 Files oder ganze Ordner hinzufügen.

Die Dateien auswählen

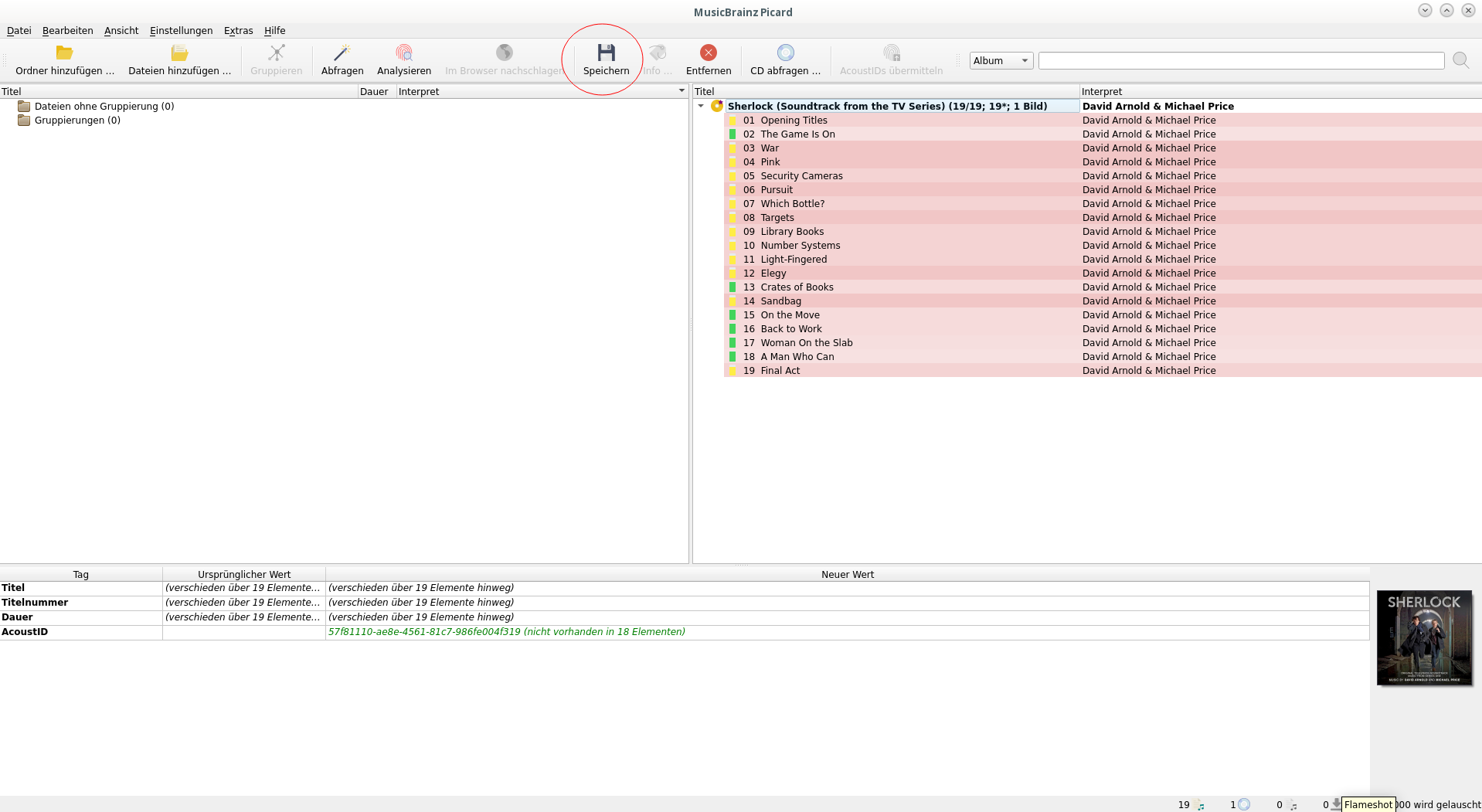
Die Dateien werden mit verschiedenen Wahrscheinlichkeiten erkannt

Noch speichern und wir sind fertig.

Nachdem man mit Picard irgendwann, realistisch so Wochen später, fertig ist, dann erzeugt man einmal die Metadaten mit dem PVA Befehl „erneuere metadaten“ und danach kann man mit Carola auch nach „SmoothJazz“ suchen, oder was Raghesh sonst noch so gefällt 😉

Termine! Termine, nichts als Termine!

Das Mantra der Postmoderne lautet nicht „Können Sie mich hören?“ sondern „Nicht schon wieder ein Meeting“. Nun bei der Anzahl der Meetings kann Carola zwar nicht helfen, aber bei der Organisation könnte sie jetzt hilfreich werden:

„Carola erinnere mich am Dienstag um achtzehn Uhr dreißig an Linux am Dienstag“

Der obige Satz führt dazu, daß Carola „Linux am Dienstag“ in die Termindatenbank aufnimmt und einen am nächsten Dienstag um 18:30 Uhr an unseren Treff „Linux am Dienstag“ erinnert. Genauso gut kann man den Tag weglassen oder „morgen“, „Übermorgen“ usw. verwenden. Da die Woche nur 7 Tage hat, können wir so nur rund eine Woche abdecken. Die Angabe des Datums fehlt noch. Der Satz:

„Carola erinnere mich um achtzehn Uhr dreißig an Linux am Dienstag“

ist auch völlig valide und meint implizit HEUTE ABEND um 18:30 Uhr.

„Carola meine Termine bitte“ oder etwas unhöflicher „Carola meine Termine“ führt dann zu einer sprachlichen Auflistung der Termine. Löschen kann man die Termine noch nicht, da die Analyse des Datums im Code noch fehlt.

„Computer?“

Wem Carola als Name nicht gefällt, oder jemand einfach das vollständige Star Trek Feeling haben will, der kann den PVA jetzt per Befehl umbenennen 🙂

„Carola Dein neuer Name lautet computer“

Gleich danach hört Euer PVA auf den Namen „Computer“. Auf Spielchen mit „Siri“,“ok Google“ oder „Hallo Alexa“ würde ich verzichten, das beeindruckt Besucher kein bisschen 😉

Medienplayer wie MPV oder Celluloid

Wer den Artikel über die neue Mediaplayersteuerung noch nicht gelesen hat, der finden den hier:

Carola: Netflix & Mediaplayerkontrolle

Kleiner Ausblick auf die nächsten Tage: Ihr bekommt einen Technikvortrag über Systemd,Timers und JAVA fails 😉

 

 

PVA – Carola spricht weiter zu uns

Posted on by

Vor ein paar Monaten haben ich einen Personal Voice Assistant(PVA), also einen persönlichen Sprachassistenten zusammengebaut. Hier ein Update zur jüngsten Entwicklung von Carola.

PVA – Carola spricht weiter zu uns

An der Sprachausgabe hat sich eine Veränderung ergeben, die dem Projekt zwar eine deutlich bessere Stimme verpaßt, aber leider auch Privatsspährenverletzungen erlaubt. Die Rede ist von der Einführung von GTTS, der Google Text-To-Speech API.Dabei werden die Textausgaben an einen Googleserver übertragen und dann in ein MP3 umgewandelt.

An sich ist das kein Problem, wenn man sich im Griff hat. Wenn aber der PVA etwas gesprochenes im Raum aufschnappt und meint, das wäre für ihn bestimmt, dann wertet er das aus. Erkennt der PVA nicht, was man von Ihm wollte, weil es unabsichtlich war, wird ein Teil des Textes zitiert. Dieser Teil, auch wenn er nur wenige Worte umfasst, würde auch an Google gehen.

Damit das nicht unwillentlich passiert, ist GTTS zwar jetzt möglich, aber nicht aktiviert. Das führt uns aber auf direktem Wege zu einem neuen coolen Feature vom PVA: Alternativen zur Laufzeit ändern, per Sprachbefehl 😀

Alternatives / Alternativen

In der Konfiguration sieht das so aus:

Es gibt eine Definition der Anwendung „say“:

app:“say„,“/usr/local/sbin/say“

Der konfigurierte Befehl wird für alle Sprachausgaben benutzt, eine Anpassung hier ändert also sofort alles. Um dies vom PVA per Sprache zu machen, sagt man bezogen auf GTTS einfach: „benutze google sprachausgabe“ und schon wird in der Konfiguration gsay, statt say eingetragen und ab sofort benutzt. Die Rückkehr zum normalen Espeak+Mbrola TTS ist entsprechend einfach: „benutzte normale sprachausgabe“.

Das sieht dann so aus:

alternatives:“normale sprachausgabe„,“say„,“/usr/local/sbin/say“
alternatives:“google sprachausgabe„,“say„,“/usr/local/sbin/gsay“

Das gleiche kann man für alle Apps machen, sofern man da Alternativen konfiguriert hat und welche die gleichen Argumente akzeptieren: Beispiel

app:“searchengine„,“duckduckgo“

alternatives:“duckduckgo„,“searchengine„,“duckduckgo“
alternatives:“googlesuche„,“searchengine„,“google“

Die Suchmaschinen sind wiederum so definiert:

searchengines:“duckduckgo„,“https://html.duckduckgo.com/html?q=<query>“
searchengines:“google„,“https://www.google.com/search?q=<query>“

In der Defaultkonfiguration sind entsprechende Beispiele konfiguriert.

Anwendungen starten

Die Liste der Apps kann jetzt beliebig erweitert werden. Der Sprachbefehl „starte runes of magic“ wird jetzt über die Appliste und nicht mehr im Javacode gestartet:

app:“runes of magic„,“runesofmagic“
app:“blender“,“blender“
app:“wetter“,“gnome-weather“
app:“karte“,“gnome-maps“
app:“firefox“,“firefox“
app:“netflix„,“firefox https://www.netflix.com/browse/my-list“
usw.

Wie man sieht, kann man auch die NetFlix Webanwendung starten, wenn man das Profile angibt und ein eigenes Profil für Netflix benutzt, kann man es auch gleich im Fullscreenkioskmodus starten, was echt stylish ist 😉 Für „Runes of Magic“ habe ich mir ein kleines Startscript gebaut, deswegen sieht das so einfach aus:

#!/bin/bash

env WINEPREFIX="/home/<username>/.wine" /opt/wine-staging/bin/wine C:\\\\windows\\\\command\\\\start.exe /d "/home/<username>/Programme/GameforgeLive/Games/DEU_deu/Runes Of Magic/" /Unix "/home/<username>/Programme/GameforgeLive/Games/DEU_deu/Runes Of Magic/launcher.exe" NoCheckVersion 1>/dev/null 2>/dev/null &

Gerade eben, beim Schreiben des Textes hatte ich die geniale Idee, wie man das gesamte System, also alle Desktop Apps automatisch ansprechen könnte …Das wird ein Spaß 😀

Checkt mal in den nächsten Tagen das Github-Repo für ein Update des PVA.java . Das kann eigentlich nicht lange dauern bis das läuft. Es würde da eher an der Spracherkennung happern, die Cache z.b. als Cash erkennt. Vermutlich ist es besser, die deutschen Programmnamen zu verwenden 😉

… GEHT 😀

Das ist sooo cool, daß ich Euch ein Video machen muß, leider streikt OpenShot gerade 🙁 . Man lässt z.b. Bilder suchen und kann diese dann mit einer Wunsch Anwendung öffnen. Er findet auch alle Programme, die ein Desktopfile haben und kann die starten bzw. die als Ziel für z.b. Bildersuchergebnisse benutzen.

Erster Beitrag:

Mbrola – etwas bessere Sprachsynthese

Lösung: Das 3n+1 Problem

Posted on by

Stand: 28.11.2021

Es gibt so mathematische Spielereien, mit denen sich hochbezahlte Köpfe Ihr Leben lang beschäftigen ohne zum Ende zu kommen. Weil es angeblich spannende Fragen sind. Weil die Fragen nicht gelöst werden können, lobt man dafür sogar Belohnungen aus. Eins der Probleme schauen wir uns kurz an und lösen dann mal auf:

Lösung: Das 3n+1 Problem

Die Funktion um die es heute geht ist ein Algorithmus, weniger eine Funktion: f(x)=3x+1 ? x/2

In Worten: Wenn x ungerade ist, gilt x=3x+1. Wenn x gerade ist, dann gilt x = x/2 .

Die Behauptung:

Für alle Ganzzahlen n>0 gilt, daß am Ende des Algorithmusses eine Zahlenschleifen von 4,2,1 rauskommt. Es gibt keine anderen Schleifen. Was zu beweisen ist.

Beispiele:

Ausgabeformat:  Anfangszahl: X-Wert big = größte Zahl in der Kette

1: x=4 big=4
1: x=2 big=4
1: x=1 big=4
1: x=4 big=4
1: x=2 big=4
1: x=1 big=4

Erklärt:

1 ist ungerade => 1*3+1 = 4
4 ist gerade => 4/2 = 2
2 ist gerade => 2/2 = 1

Man sieht, daß hier eine Schleife 4,2,1 rauskommt, weil bei x=1 das Ergebnis wieder 4 ist. In der Programmierung ist das eine Endlosschleife, weil die Abbruchbedingung fehlt. Deswegen stoppen alle nachfolgenden Ausgaben auch bei 1.

Anfangszahl 2:

2: x=1 big=1

Da muß man nicht viel erklären, weil steht oben schon 😉

3: x=10 big=10
3: x=5 big=10
3: x=16 big=16
3: x=8 big=16
3: x=4 big=16
3: x=2 big=16
3: x=1 big=16

Auch hier 4,2,1

4: x=2 big=2
4: x=1 big=2

Oh.. eine 4.. wie in 4,2,1.. ähm ja. siehe oben

5: x=16 big=16
5: x=8 big=16
5: x=4 big=16
5: x=2 big=16
5: x=1 big=16
6: x=3 big=3
6: x=10 big=10
6: x=5 big=10
6: x=16 big=16
6: x=8 big=16
6: x=4 big=16
6: x=2 big=16
6: x=1 big=16
7: x=22 big=22
7: x=11 big=22
7: x=34 big=34
7: x=17 big=34
7: x=52 big=52
7: x=26 big=52
7: x=13 big=52
7: x=40 big=52
7: x=20 big=52
7: x=10 big=52
7: x=5 big=52
7: x=16 big=52
7: x=8 big=52
7: x=4 big=52
7: x=2 big=52
7: x=1 big=52
8: x=4 big=4
8: x=2 big=4
8: x=1 big=4
9: x=28 big=28
9: x=14 big=28
9: x=7 big=28
9: x=22 big=28
9: x=11 big=28
9: x=34 big=34
9: x=17 big=34
9: x=52 big=52
9: x=26 big=52
9: x=13 big=52
9: x=40 big=52
9: x=20 big=52
9: x=10 big=52
9: x=5 big=52
9: x=16 big=52
9: x=8 big=52
9: x=4 big=52
9: x=2 big=52
9: x=1 big=52

Das läßt sich beliebig für jede Ganzzahl n > 0 wiederholen.

Diese Auflistungen hier zeigen schon den Grund für das Verhalten und das ist wenig mystisch und noch weniger unerklärlich.

Die Auflösung:

Die Frage war: Wieso kommt am Ende immer eine Schleife mit ( 4,2,1 ) raus?

Das ist ganz leicht, weil 3x+1 für jedes Start-x irgendwann auf 2^n trifft. 2^n ist die folgende Operation : 2*2*2*2*2*2*2….*2 . Das ist genau das Gegenteil von der Berechnung für gerade Zahlen in dem Algorithmus ( x=x/2 ) . Wenn ich also z.b. 2^6 treffe, was 64 ist, und dies ständig durch 2 teile, kommt am Ende ohne Zweifel 1 raus. Es ist egal wie groß n ist, das gilt immer. Der Algorithmus endet also immer in der Sequenz ( 2^n , 2^(n-1) … 2^(n-n) und 2^(0) = 1 . Da 1*3+1 = 2^2 ist, terminiert der Algorithmus nicht und es kommt zur Endlosschleife.

Das ist absolut kein Wunder.

Die nächste Behauptung ist: es gibt keine anderen Schleifen.

Da 3x+1 ausschließlich bei ungeraden Zahlen angewendet wird und bei der Berechnung garantiert immer eine gerade Zahl herauskommt und nicht jede gerade Zahl eine Potenz von 2 ist, kann es keine anderen Schleifen geben, da bei jedem Schritt nach einer ungeraden Zahl die Teilung durch 2 solange stattfindet, bis wieder eine ungerade Zahl kommt.

Da es für jede Potenz 2^n für n > 1 eine ungerade Zahlen x gibt, die x = (2^n -1) / 3 erfüllt, kann es keine andere Schleife geben, denn jede gerade Zahl geteilt durch 2 trifft am Ende der Teilung gerader Zahlen immer auf eine ungerade Zahl und sobald diese ungerade Zahl 1 ist, ist die Schleifenbedingung erfüllt. Da eine ungerade Zahl verdreifacht wird(+1), aber eine gerade Zahl nur halbiert, wächst x über die Zeit im Schnitt an, bis x = 2^n ist, also eine 2er Potenz getroffen wird. QED.

Negative Startwerte

Bei negativen Startwerten kommt es ganz schnell zu Zahlenschleifen. Das liegt nach Analyse des Algorithmuses an einem BUG. Wenn das ein Programm wäre, würde ich dafür eine 6 vergeben und es dem Entwickler um die Ohren hauen 😉

Die Formel ist ja „3x+1“. Diese Formel kann für einige Ganzzahlen keine 2er Potenzen im negativen Zahlenstrahl finden. Der „Bug“ liegt im „+“ Zeichen, daß im negativen Zahlenraum zum „Fehlerfall“ führt. Es müßte nämlich eigentlich „3x-1“ lauten. Damit erreicht man im negativen Zahlenbereich eine exakte Spiegelung des positiven Zahlenraumes, weil alle oben genannten Bedingungen dann erfüllt sind.

Das liegt an der Verletzung der Gleichungsregel, daß wenn ich auf der einen Seite der Gleichung etwas abziehe, ich es zum Ausgleich auf der anderen Seite hinzufügen muß:

2 = 5-3 => 2+3 = 5

Der Algorithmus „verletzt“ dies beim Übergang von positiven zu negativen Startzahlen. Das ist sprach-mathematisch natürlich inkorrekt, beschreibt aber das Problem sehr gut.

Beispiel:

x = -21

x = -63 / 3

x*3 = -63 = -62 -1

x*3+1 = -62

Wenn man das jetzt für +21 macht, gilt:

21*3+1 = 64

64 = 2^6 also durch 2 bis zur 1 teilbar. Für -62 gilt das nicht, da kommt bei unserem Algorithmus -31 raus, statt -32 wie es nötig wäre um zu terminieren.

Fazit

Das der Algorithmus im Negativen Zahlenbereich „mysteriöse Schleifen“ bildet, im positiven Bereich aber nicht, ist also ein Fehler im Algorithmus und nicht „mysteriös“, wie einige Youtuber das andeuten. Er ist einfach schlecht gemacht worden 😀

Kommentare sind erlaubt, also tobt Euch aus 😉

Wieviel Zeit und Energie in das angebliche Problem eines defekten Algorithmuses verplempert wird und wurde, könnt Ihr hier nachlesen:

https://en.wikipedia.org/wiki/Collatz_conjecture#Iterating_on_all_integers

oder lasst es Euch hier „erklären“:

Ich kann mich den Matheprofs nur anschließen: Verplempert keine Zeit damit, es ist einfach nur ein kaputter Algorithmus.

Nicht „3x+1“ ist das Problem, sondern der Algorithmus an sich ist defekt. Wie man sich daran so aufgeilen kann wie im obigen Beitrag ist mir persönlich ein Rätsel. Solche Fehler kommen in der Programmierung laufend vor, weil einer bei der Umsetzung oder der Planung geschlafen hat.

Hier ein kleines Programm für Java, das bei evtl. doch stattfindenden Versuchen hilfreich sein kann. Der BUG ist darin aber schon behoben worden 😉



public class ThreeXPlusOne {


	static public void main(String[] args) {
	
		long x = 0;
		long max = 99;
		
		for(long n=-max;n<max;n++) { x = n; long big = 0; if ( n != 0 ) do { if ( (x/2)*2 == x ) { x = x/2; } else { if ( n > 0 ) {
						x = 3*x+1;
					} else  x = 3*x-1; // Korrektur für n<0 weil, mit +1 kann man nie 2^n treffen } if ( n > 0 && x > big ) big = x;
				if ( n < 0 && x < big ) big = x; if ( args.length > 0 ) System.out.println( n+": x="+x+" big="+big);

			} while ( x != -1 && x != 1 && x!=n );
			
			if ( args.length == 0 ) System.out.println( n+": x="+x+" big="+big);
		}	
	}
}

Ihr werdet den Code noch einem Beautyfier übergeben müssen, weil WordPress den unbedingt umformatieren muß ( und ich keine Lust habe, deswegen in der WordPressdatenbank den Code direkt einzutragen ).